Codeforces Round #686 (Div.3) 解题报告

A. Special Permutation

水题，只需要总体移一位即可。

#include <bits/stdc++.h>
#define ll long long
#define ls id << 1
#define rs id << 1 | 1
#define mem(array, value, size, type) memset(array, value, ((size) + 5) * sizeof(type))
#define memarray(array, value) memset(array, value, sizeof(array))
#define fillarray(array, value, begin, end) fill((array) + (begin), (array) + (end) + 1, value)
#define fillvector(v, value) fill((v).begin(), (v).end(), value)
#define pb(x) push_back(x)
#define st(x) (1LL << (x))
#define pii pair<int, int>
#define mp(a, b) make_pair((a), (b))
#define Flush fflush(stdout)
#define vecfirst (*vec.begin())
#define veclast (*vec.rbegin())
#define vecall(v) (v).begin(), (v).end()
#define vecupsort(v) (sort((v).begin(), (v).end()))
#define vecdownsort(v, type) (sort(vecall(v), greater<type>()))
#define veccmpsort(v, cmp) (sort(vecall(v), cmp))
using namespace std;
const int N = 500050;
const int inf = 0x3f3f3f3f;
const ll llinf = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
clock_t TIME__START, TIME__END;
void program_end()
{
#ifdef ONLINE
    printf("\n\nTime used:
    system("pause");
#endif
}
int n;

inline void solve()
{
    scanf(
    for (int i = 1; i < n; ++i)
        printf(
    puts("1");
}

int main()
{
    TIME__START = clock();
    int Test = 1;
    scanf(
    while (Test--)
    {
        solve();
        // if (Test)
        //     putchar('\n');
    }
    TIME__END = clock();
    program_end();
    return 0;
}

---

B. Unique Bid Auction

按照题意模拟即可。

#include <bits/stdc++.h>
#define ll long long
#define ls id << 1
#define rs id << 1 | 1
#define mem(array, value, size, type) memset(array, value, ((size) + 5) * sizeof(type))
#define memarray(array, value) memset(array, value, sizeof(array))
#define fillarray(array, value, begin, end) fill((array) + (begin), (array) + (end) + 1, value)
#define fillvector(v, value) fill((v).begin(), (v).end(), value)
#define pb(x) push_back(x)
#define st(x) (1LL << (x))
#define pii pair<int, int>
#define mp(a, b) make_pair((a), (b))
#define Flush fflush(stdout)
#define vecfirst (*vec.begin())
#define veclast (*vec.rbegin())
#define vecall(v) (v).begin(), (v).end()
#define vecupsort(v) (sort((v).begin(), (v).end()))
#define vecdownsort(v, type) (sort(vecall(v), greater<type>()))
#define veccmpsort(v, cmp) (sort(vecall(v), cmp))
using namespace std;
const int N = 500050;
const int inf = 0x3f3f3f3f;
const ll llinf = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
clock_t TIME__START, TIME__END;
void program_end()
{
#ifdef ONLINE
    printf("\n\nTime used:
    system("pause");
#endif
}
int n, a[N], cnt[N], id[N];

inline void solve()
{
    mem(cnt, 0, n, int);
    scanf(
    for (int i = 1; i <= n; ++i)
        scanf(
    int ans = -1;
    for (int i = 1; i <= n; ++i)
    {
        if (cnt[i] == 1)
        {
            ans = id[i];
            break;
        }
    }
    cout << ans << '\n';
}

int main()
{
    TIME__START = clock();
    int Test = 1;
    scanf(
    while (Test--)
    {
        solve();
        // if (Test)
        //     putchar('\n');
    }
    TIME__END = clock();
    program_end();
    return 0;
}

---

C. Sequence Transformation

把所有相邻且相同的项合并起来，答案就是每个元素出现最少的次数。注意两头因为不需要删除，两头的次数元素减一下出现次数即可。
答案就是 $\min(cnt_i)+1$

#include <bits/stdc++.h>
#define ll long long
#define ls id << 1
#define rs id << 1 | 1
#define mem(array, value, size, type) memset(array, value, ((size) + 5) * sizeof(type))
#define memarray(array, value) memset(array, value, sizeof(array))
#define fillarray(array, value, begin, end) fill((array) + (begin), (array) + (end) + 1, value)
#define fillvector(v, value) fill((v).begin(), (v).end(), value)
#define pb(x) push_back(x)
#define st(x) (1LL << (x))
#define pii pair<int, int>
#define mp(a, b) make_pair((a), (b))
#define Flush fflush(stdout)
#define vecfirst (*vec.begin())
#define veclast (*vec.rbegin())
#define vecall(v) (v).begin(), (v).end()
#define vecupsort(v) (sort((v).begin(), (v).end()))
#define vecdownsort(v, type) (sort(vecall(v), greater<type>()))
#define veccmpsort(v, cmp) (sort(vecall(v), cmp))
using namespace std;
const int N = 500050;
const int inf = 0x3f3f3f3f;
const ll llinf = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
clock_t TIME__START, TIME__END;
void program_end()
{
#ifdef ONLINE
    printf("\n\nTime used:
    system("pause");
#endif
}
int n, a[N], cnt[N], b[N];

inline void solve()
{
    mem(a, 0, n, int);
    mem(cnt, 0, n, int);
    int ans = inf;
    scanf(
    for (int i = 1; i <= n; ++i)
        scanf(
    int m = 0;
    for (int i = 1; i <= n; ++i)
    {
        if (a[i] == b[m])
            continue;
        b[++m] = a[i];
    }
    if (m == 1)
        return puts("0"), void();
    for (int i = 1; i <= m; ++i)
        cnt[b[i]]++;
    cnt[b[1]]--, cnt[b[m]]--;
    for (int i = 1; i <= m; ++i)
        ans = min(ans, cnt[b[i]] + 1);
    printf(
}

int main()
{
    TIME__START = clock();
    int Test = 1;
    scanf(
    while (Test--)
    {
        solve();
        // if (Test)
        //     putchar('\n');
    }
    TIME__END = clock();
    program_end();
    return 0;
}

---

D. Number into Sequence

将 $n$ 分解质因数，不难发现答案其实就是某个质数的幂次的最大值。即：$n=p_1^{m_1}p_2^{m_2}p_3^{m_3}...$，那么答案就是 $\max(m_1,m_2,m_3,...)$.
构造方法也很简单，先取这个质数 $m_i-1$ 次，然后剩下所有的质数乘起来放在最后面即可。

#include <bits/stdc++.h>
#define ll long long
#define ls id << 1
#define rs id << 1 | 1
#define mem(array, value, size, type) memset(array, value, ((size) + 5) * sizeof(type))
#define memarray(array, value) memset(array, value, sizeof(array))
#define fillarray(array, value, begin, end) fill((array) + (begin), (array) + (end) + 1, value)
#define fillvector(v, value) fill((v).begin(), (v).end(), value)
#define pb(x) push_back(x)
#define st(x) (1LL << (x))
#define pii pair<int, int>
#define mp(a, b) make_pair((a), (b))
#define Flush fflush(stdout)
#define vecfirst (*vec.begin())
#define veclast (*vec.rbegin())
#define vecall(v) (v).begin(), (v).end()
#define vecupsort(v) (sort((v).begin(), (v).end()))
#define vecdownsort(v, type) (sort(vecall(v), greater<type>()))
#define veccmpsort(v, cmp) (sort(vecall(v), cmp))
using namespace std;
const int N = 500050;
const int inf = 0x3f3f3f3f;
const ll llinf = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
clock_t TIME__START, TIME__END;
void program_end()
{
#ifdef ONLINE
    printf("\n\nTime used:
    system("pause");
#endif
}
ll n;
vector<pair<ll, int>> vecpri;
vector<ll> ans;

inline void solve()
{
    ans.resize(0);
    vecpri.resize(0);
    scanf(
    ll m = n;
    for (ll i = 2; i * i <= n; ++i)
    {
        if (n
        {
            int cnt = 0;
            while (n
                n /= i, cnt++;
            vecpri.push_back({i, cnt});
        }
    }
    if (n > 1)
        vecpri.push_back({n, 1});
    int mxi = 0;
    for (int i = 0; i < (int)vecpri.size(); ++i)
    {
        if (vecpri[i].second > vecpri[mxi].second)
            mxi = i;
    }
    while (vecpri[mxi].second > 1)
        ans.push_back(vecpri[mxi].first), vecpri[mxi].second--, m /= vecpri[mxi].first;
    ans.push_back(m);
    cout << ans.size() << '\n';
    for (auto i : ans)
        cout << i << ' ';
    putchar('\n');
}

int main()
{
    TIME__START = clock();
    int Test = 1;
    scanf(
    while (Test--)
    {
        solve();
        // if (Test)
        //     putchar('\n');
    }
    TIME__END = clock();
    program_end();
    return 0;
}

---

E. Number of Simple Paths

刚开始还以为是任意一个无向图......我寻思这个也没法做啊（
后来才发现是基环树，那没事了。
有一个结论就是对于一个 $n$ 个节点的树，简单路径数为 $\frac{n(n-1)}{2}$，然后基环树上每一棵以环上的点为根的子树就可以先根据这个统计自己的贡献。
然后再考虑带上环的贡献。实际上就是一棵树到另一棵树的路径数。因为在环上走有顺时针逆时针两个方向，所以对于两棵树的贡献来说，就是其 $size$ 的积。
最后所有贡献全都加起来，这个题就做完了~

#include <bits/stdc++.h>
#define ll long long
#define ls id << 1
#define rs id << 1 | 1
#define mem(array, value, size, type) memset(array, value, ((size) + 5) * sizeof(type))
#define memarray(array, value) memset(array, value, sizeof(array))
#define fillarray(array, value, begin, end) fill((array) + (begin), (array) + (end) + 1, value)
#define fillvector(v, value) fill((v).begin(), (v).end(), value)
#define pb(x) push_back(x)
#define st(x) (1LL << (x))
#define pii pair<int, int>
#define mp(a, b) make_pair((a), (b))
#define Flush fflush(stdout)
#define vecfirst (*vec.begin())
#define veclast (*vec.rbegin())
#define vecall(v) (v).begin(), (v).end()
#define vecupsort(v) (sort((v).begin(), (v).end()))
#define vecdownsort(v, type) (sort(vecall(v), greater<type>()))
#define veccmpsort(v, cmp) (sort(vecall(v), cmp))
using namespace std;
const int N = 500050;
const int inf = 0x3f3f3f3f;
const ll llinf = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
clock_t TIME__START, TIME__END;
void program_end()
{
#ifdef ONLINE
    printf("\n\nTime used:
    system("pause");
#endif
}
ll ans;
int n;
vector<int> e[N];
int pre[N];
bool found_cir;
bool vis[N];
int huan_fir_node;
int siz[N];

void dfs(int u, int fa)
{
    vis[u] = 1;
    for (auto v : e[u])
    {
        if (v == fa)
            continue;
        pre[v] = u;
        if (vis[v])
        {
            found_cir = true;
            huan_fir_node = v;
            return;
        }
        dfs(v, u);
        if (found_cir)
            return;
    }
}

void dfs2(int root, int u, int fa)
{
    siz[root]++;
    for (auto v : e[u])
    {
        if (v == fa || vis[v])
            continue;
        dfs2(root, v, u);
    }
}

inline void solve()
{
    ans = 0;
    scanf(
    mem(pre, 0, n, int);
    for (int i = 0; i <= n; ++i)
        e[i].resize(0);
    for (int i = 1; i <= n; ++i)
    {
        int x, y;
        scanf(
        e[x].push_back(y);
        e[y].push_back(x);
    }
    mem(vis, 0, n, bool);
    found_cir = 0;
    dfs(1, 0);
    vector<int> vec_huan_node;
    mem(vis, 0, n, bool);
    mem(siz, 0, n, int);
    for (int u = huan_fir_node; !vis[u]; u = pre[u])
    {
        vis[u] = 1;
        vec_huan_node.push_back(u);
    }
    ll sumsiz = 0;
    for (auto u : vec_huan_node)
    {
        dfs2(u, u, 0);
        ans += 1ll * (siz[u] - 1ll) * siz[u] / 2;
        sumsiz += siz[u];
    }
    for (auto u : vec_huan_node)
    {
        ans += 1ll * siz[u] * (sumsiz - siz[u]);
    }
    printf(
}

int main()
{
    TIME__START = clock();
    int Test = 1;
    scanf(
    while (Test--)
    {
        solve();
        // if (Test)
        //     putchar('\n');
    }
    TIME__END = clock();
    program_end();
    return 0;
}

---

F. Array Partition

可以先枚举 x，这样我们可以知道当前这个三者需要相等的值就是 premx，即当前前缀最大值。
接下来，根据这个 premx 可以先把最后一段给确定下来。当然目前也只能确定一个范围，接下来考虑如何找到一个具体的端点值。
还是来画个图来看吧：

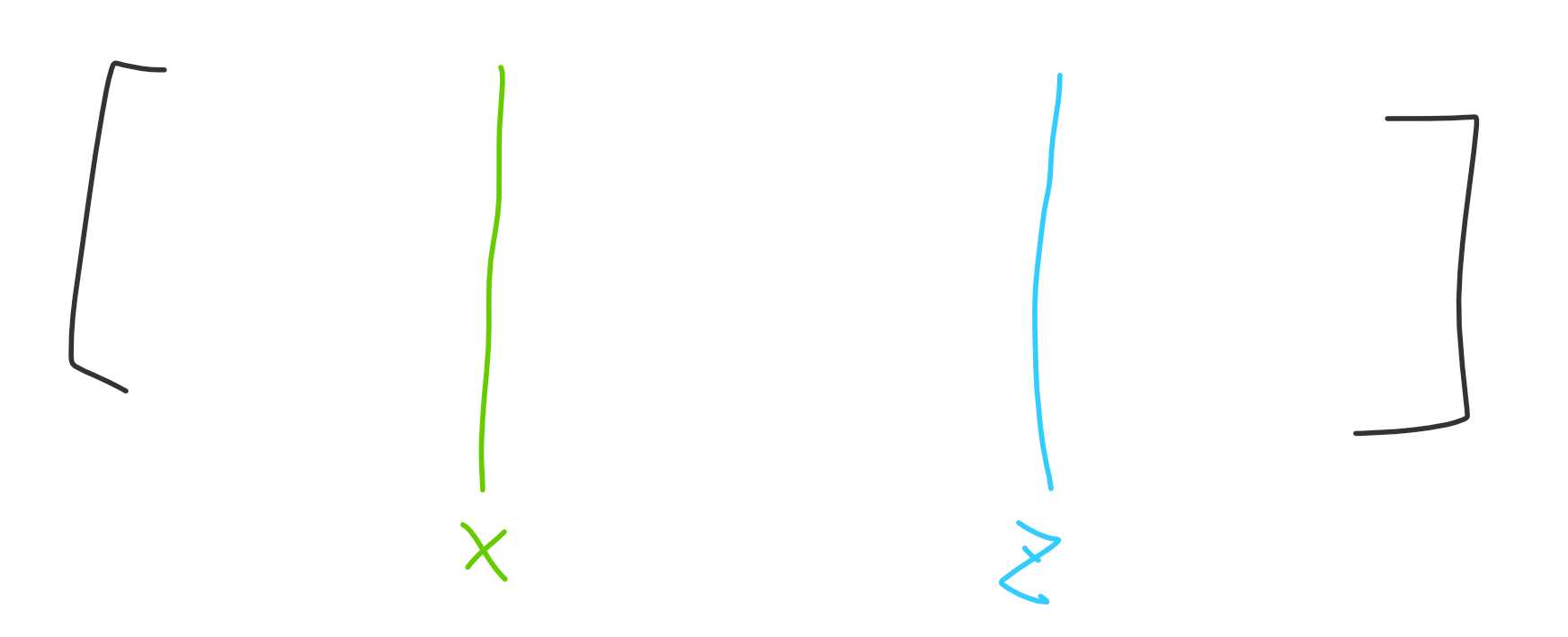
z 就是对应的最右边的位置，满足 a[z]=premx。当然，x 和 z 中间可能还会有一个比 premx 更大的值。同样地，设 l 是最右边的且在 z 左边的满足 a[l]>premx 的位置。像下图这样：

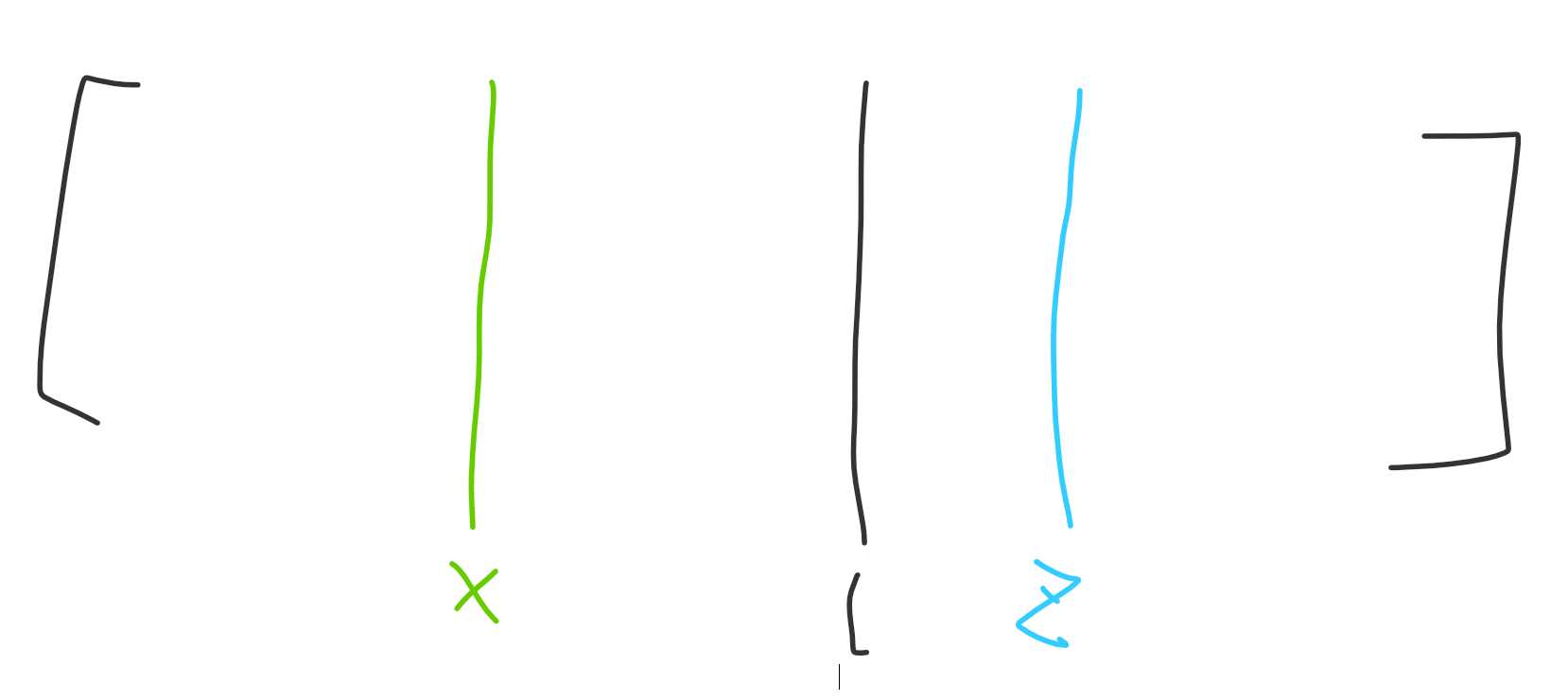
这样这个区间被划分成了 4 段。首先 check：$\min(x+1,l)$ 与 premx 的大小关系：
如果等于，真棒，那就找到了一个答案，把 z 设为 l+1 即可（当然这个 z 不是题干中的 z）；
如果小于，那就说明肯定不可能找到一个端点使得中间这段的最小值还更大，直接 continue；
如果大于，好，接下来还需要进一步的讨论，往下看。

---

实际上这个时候重点在于 [l,z-1] 这一段。我们想找到一个端点，这个端点的值正好是 premx，设为 r，并且区间 [l,r] 的最小值也应该等于 premx。不难发现，这个端点越靠近 l 越好，于是这里只需要一个二分就可以找到这个端点。找到了的话就像下图这样：

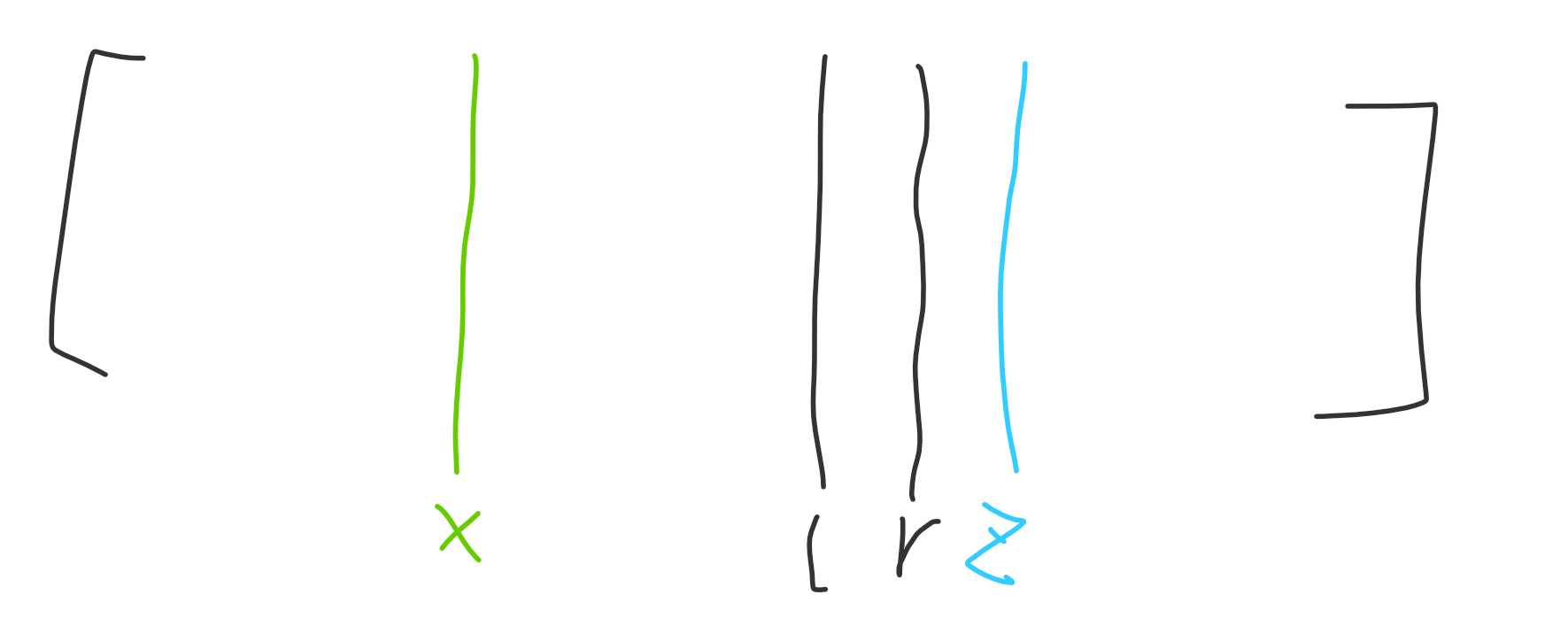
接下来就像上面说的，check 一下 [l,r] 的最小值是否为 premx。如果是，很好，又找到了，把 z 设为 r+1 即可；没有，那就回到第一步，继续枚举 x。
综上，这个题就做完了。区间最小值可以用线段树或者 st 表，时间复杂度约为 $\mathcal{O}(n\log^2n)$。

#include <bits/stdc++.h>
#define ll long long
#define ls id << 1
#define rs id << 1 | 1
#define mem(array, value, size, type) memset(array, value, ((size) + 5) * sizeof(type))
#define memarray(array, value) memset(array, value, sizeof(array))
#define fillarray(array, value, begin, end) fill((array) + (begin), (array) + (end) + 1, value)
#define fillvector(v, value) fill((v).begin(), (v).end(), value)
#define pb(x) push_back(x)
#define st(x) (1LL << (x))
#define pii pair<int, int>
#define mp(a, b) make_pair((a), (b))
#define Flush fflush(stdout)
#define vecfirst (*vec.begin())
#define veclast (*vec.rbegin())
#define vecall(v) (v).begin(), (v).end()
#define vecupsort(v) (sort((v).begin(), (v).end()))
#define vecdownsort(v, type) (sort(vecall(v), greater<type>()))
#define veccmpsort(v, cmp) (sort(vecall(v), cmp))
using namespace std;
const int N = 500050;
const int inf = 0x3f3f3f3f;
const ll llinf = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
clock_t TIME__START, TIME__END;
void program_end()
{
#ifdef ONLINE
    printf("\n\nTime used:
    system("pause");
#endif
}
int n, a[N], sufmx[N];
map<int, vector<int>> mp_vec;
map<int, int> mp_sufmx_pos;
struct segtree
{
    int l, r, mn;
} t[N << 2];
inline void pushup(int id) { t[id].mn = min(t[ls].mn, t[rs].mn); }
void build(int l, int r, int id)
{
    t[id].mn = 0;
    t[id].l = l, t[id].r = r;
    if (l == r)
    {
        t[id].mn = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(l, mid, ls);
    build(mid + 1, r, rs);
    pushup(id);
}
int query(int L, int R, int id)
{
    if (L > R)
        return inf;
    int l = t[id].l, r = t[id].r;
    if (L <= l && R >= r)
        return t[id].mn;
    int mid = (l + r) >> 1;
    if (R <= mid)
        return query(L, R, ls);
    else if (L > mid)
        return query(L, R, rs);
    else
        return min(query(L, mid, ls), query(mid + 1, R, rs));
}

inline void solve()
{
    scanf(
    mem(sufmx, 0, n, int);
    for (int i = 1; i <= n; ++i)
        scanf(
    build(1, n, 1);
    mp_vec.clear();
    mp_sufmx_pos.clear();
    mp_sufmx_pos.insert({inf, 0});
    for (int i = 1; i <= n; ++i)
        mp_vec[a[i]].push_back(i);
    for (int i = n; i; --i)
    {
        sufmx[i] = max(sufmx[i + 1], a[i]);
        if (mp_sufmx_pos.find(sufmx[i]) == mp_sufmx_pos.end())
            mp_sufmx_pos.insert({sufmx[i], i});
        else
            continue;
    }
    int premx = 0;
    for (int x = 1; x <= n; ++x)
    {
        premx = max(premx, a[x]);
        if (mp_sufmx_pos.find(premx) == mp_sufmx_pos.end() || mp_sufmx_pos[premx] <= x + 1)
            continue;
        int z = mp_sufmx_pos[premx];
        auto it = mp_sufmx_pos.find(premx);
        it++;
        int l = max((*it).second, x + 1) + 1;
        int mn = query(x + 1, l - 1, 1);
        if (mn < premx)
            continue;
        else if (mn == premx)
        {
            z = l;
            printf("YES\
            return;
        }
        else
        {
            auto r = lower_bound(mp_vec[premx].begin(), mp_vec[premx].end(), l);
            if (r == mp_vec[premx].end() || (*r) >= z)
                continue;
            mn = query(l, *r, 1);
            if (mn == premx)
            {
                z = (*r) + 1;
                printf("YES\
                return;
            }
        }
    }
    puts("NO");
}

int main()
{
    TIME__START = clock();
    int Test = 1;
    scanf(
    while (Test--)
    {
        solve();
        // if (Test)
        //     putchar('\n');
    }
    TIME__END = clock();
    program_end();
    return 0;
}