对于每一颗星星,当成点光源,求其对于每一个线段在 $x$ 轴上的投影即可。投影是一个个区间,对于每一颗星,先对这些区间求一次区间并,之后对于所有并之后的区间求一次区间交,交集区间的总长度就是答案。这个过程用 map 就行。
但麻烦就在于这个往 $x$ 轴的投影......要把人搞吐。
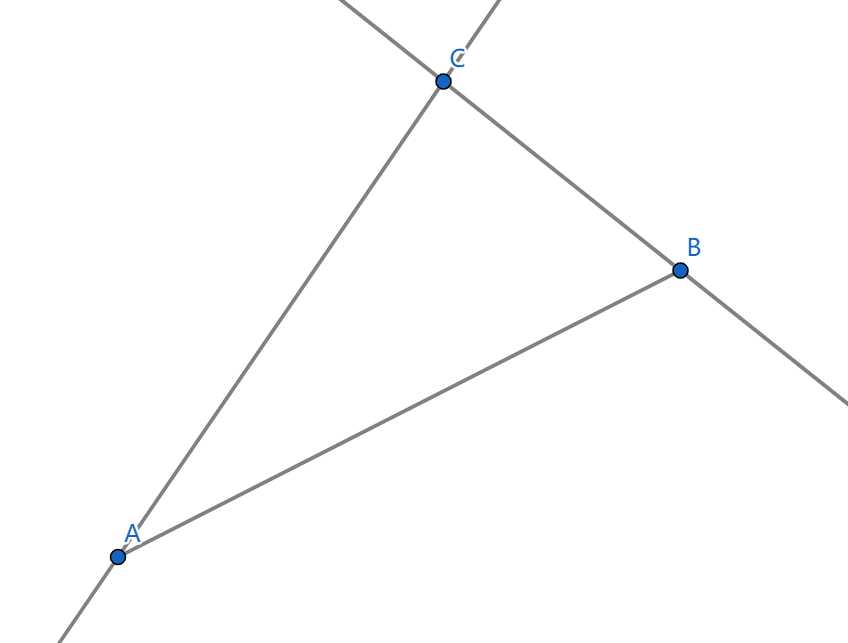
总的来说分成好几种情况(AB 是线段,C 是星星):
- 这种最直接,投影下去就行
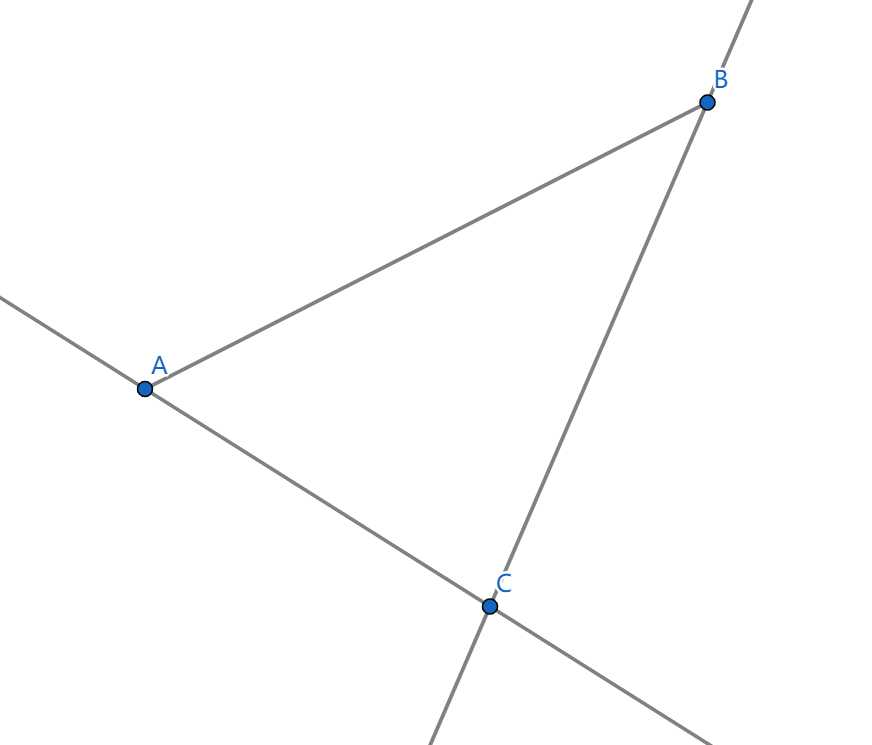
- 这种也还好,直接无视就行
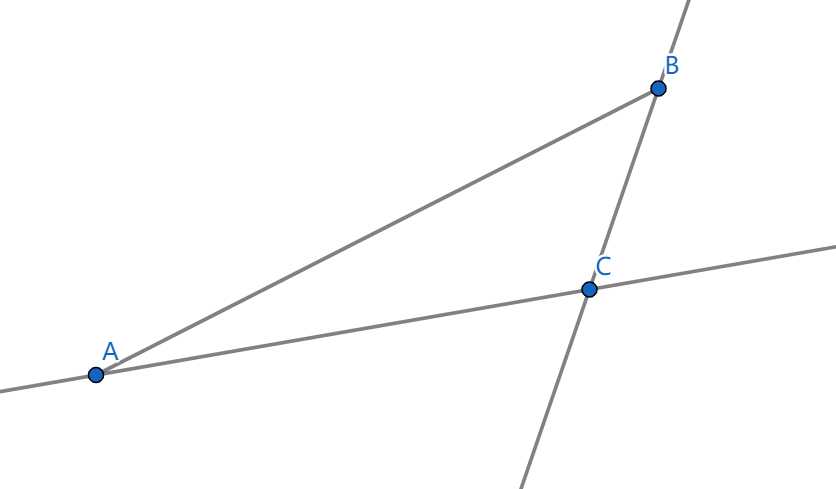
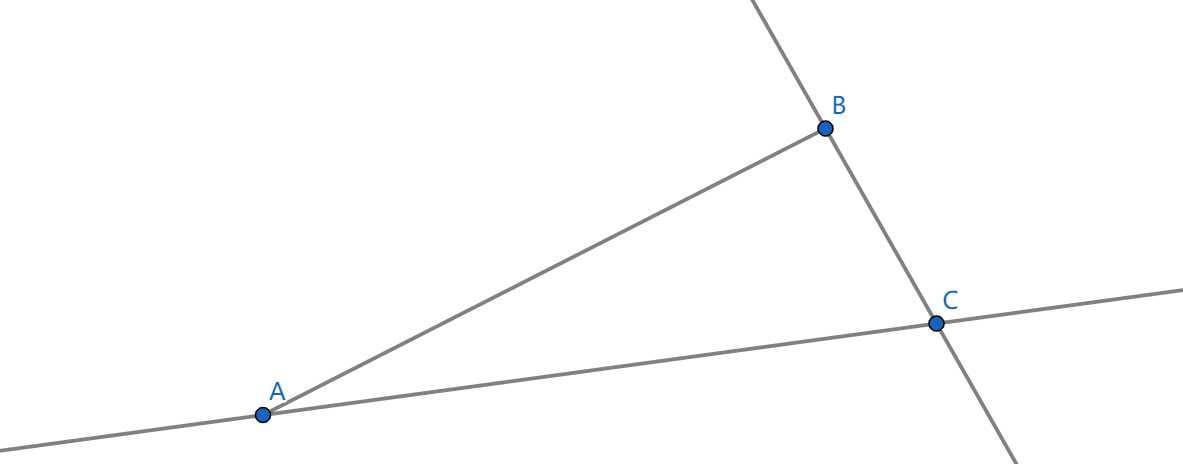
- 这两种是真的麻烦......
什么意思呢?就是根据 C 点位置不同,其影响的区间是一样的,但是在代码实现过程中,要注意不要设错区间,即把 [-INF, xr] 设成 [xl, INF] 这种。
对于第三种情况其实分得比较细......我代码里面各种不等号都不能混用 QAQ
总之上代码吧(
#include <bits/stdc++.h>
#define MAXN 505
using namespace std;
const double INF = 1e10;
const double eps = 1e-7;
struct point
{
long long x, y;
point() {}
point(long long _, long long __) : x(_), y(__) {}
point operator-(const point &a) const
{
return point(x - a.x, y - a.y);
}
int operator*(const point &a) const
{
return x * a.y - y * a.x;
}
};
point p[MAXN];
int T, n, m;
inline double getInter(point A, point B)
{
// assert(B.x != A.x);
if (B.x == A.x)
return A.x;
double k = (1.0 * B.y - A.y) / (1.0 * B.x - A.x);
double b = B.y - k * B.x;
assert(fabs(k) >= eps);
return -b / k;
}
map<double, int> mp_line, mp_point[MAXN];
bool isInLine(point p, point l, point r)
{
return ((l.x - p.x) * (p.x - r.x) >= 0) && ((l.y - p.y) * (p.y - r.y) >= 0);
}
void Solve()
{
mp_line.clear();
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%lld %lld", &p[i].x, &p[i].y), mp_point[i].clear();
for (int i = 1; i <= m; i++)
{
point l, r, pl, pr;
scanf("%lld %lld %lld %lld", &l.x, &l.y, &r.x, &r.y);
if (l.x > r.x)
swap(l, r);
for (int j = 1; j <= n; j++)
{
double xl, xr;
if ((l - p[j]) * (r - p[j]) == 0)
{
if (isInLine(p[j], l, r))
xl = -INF, xr = INF;
else
continue;
}
else
{
pl = l - p[j];
pr = r - p[j];
if (pl.y >= 0)
xl = pl.x >= 0 ? INF : -INF;
else
xl = getInter(p[j], l);
if (pr.y >= 0)
xr = pr.x >= 0 ? INF : -INF;
else
xr = getInter(p[j], r);
if (fabs(fabs(xl) - INF) < eps && fabs(fabs(xr) - INF) < eps)
continue;
if (xl > xr)
swap(xl, xr);
if (l.x != r.x)
{
double k = (1.0 * r.y - l.y) / (1.0 * r.x - l.x);
double b = r.y - k * r.x;
double Y = k * p[j].x + b;
if (xl == -INF)
{
if (Y > p[j].y && pr.x >= 0)
xl = INF;
}
else if (xr == INF)
{
if (Y > p[j].y && pl.x < 0)
xr = -INF;
}
}
}
if (xl > xr)
swap(xl, xr);
mp_point[j][xl]++, mp_point[j][xr]--;
}
}
for (int i = 1; i <= n; ++i)
{
int now = 0;
for (auto j : mp_point[i])
{
if (now == 0 && j.second > 0)
{
mp_line[j.first]++;
}
else if (now + j.second == 0)
{
mp_line[j.first]--;
}
now += j.second;
}
}
double ans = 0;
int now = 0;
pair<double, int> lst;
for (auto i : mp_line)
{
if (now == n)
{
ans += i.first - lst.first;
}
now += i.second;
lst = i;
}
if (ans - 1e9 > 0)
return puts("-1"), void();
printf("%.12lf\n", ans);
}
int main()
{
scanf("%d", &T);
while (T--)
Solve();
#ifdef ONLINE
system("pause");
#endif
return 0;
}






Comments NOTHING