题目就是要我们求这个东西
$$
X=\max\limits_{i=1 ... n}\{|x_i|+|y_i|\}
$$
转化成切比雪夫坐标,即 $|x|+|y|=\max\{|x+y|,|x-y| \}$,就是这个
$$
X=\max\limits_{i=1 ... n}\{\max\{|x_i+y_i| ,|x_i-y_i| \}\}
$$
这个东西有个很漂亮的性质:$x+y,x-y$ 是相互独立的!设 $a=x+y,b=x-y$ 于是,二维平面上的随机游走,对应有 $1/2$ 的概率使得 $a=a+1$ 以及 $1/2$ 的概率使得 $a=a-1$,对于 $b$ 同理。
对于我们要求的东西就是 $X$ 的期望 $E(X)$,试着推推式子:
$$
\begin{align}
E(X)&=\sum\limits_{k=1}^{n}k\cdot P\{X=k\} \\
&= 1\cdot P\{X=1\} + 2\cdot P\{X=2\}+...+n\cdot P\{X=n\} \\
&= \sum\limits_{i=1}^{n} P\{X=i\} + \sum\limits_{i=2}^{n} P\{X=i\} + ...+\sum\limits_{i=n}^{n} P\{X=i\} \\
&= \sum \limits _ {k=1}^{n} P\{X\ge k\} \\
&= \sum \limits _ {k=1}^{n} (1-P\{X < k\}) \\
&= n - \sum \limits _ {k=1}^{n} P\{X < k\} \\
&= n - \sum \limits _ {k=1}^{n-1} P\{X \le k\} \\
\end{align}
$$
嘛其实上面都是些很基础的推式子......
然后就考虑 $P\{X \le k\}$ 怎么求。由于 $a,b$ 独立,我们只需要考虑其中一个即可。
比如我们考虑 $a$,那么此时就将二维的随机游走变成了一维的随机游走(因为二维上每走一步都对应 $a$ 的加一或减一),并且这个点必须在 $[-k,k]$ 的范围内。
这个问题怎么求解?又转成二维平面来看,设这个点在一维中往右走一格对应二维中往右走一格,而在一维中往左走一格对应二维中往上走一格,于是 $[-k,k]$ 的限制就变成了在二维中这个点被夹在 $y=x-k,y=x+k$ 这两条直线中(可以在直线上,但不能穿过)。
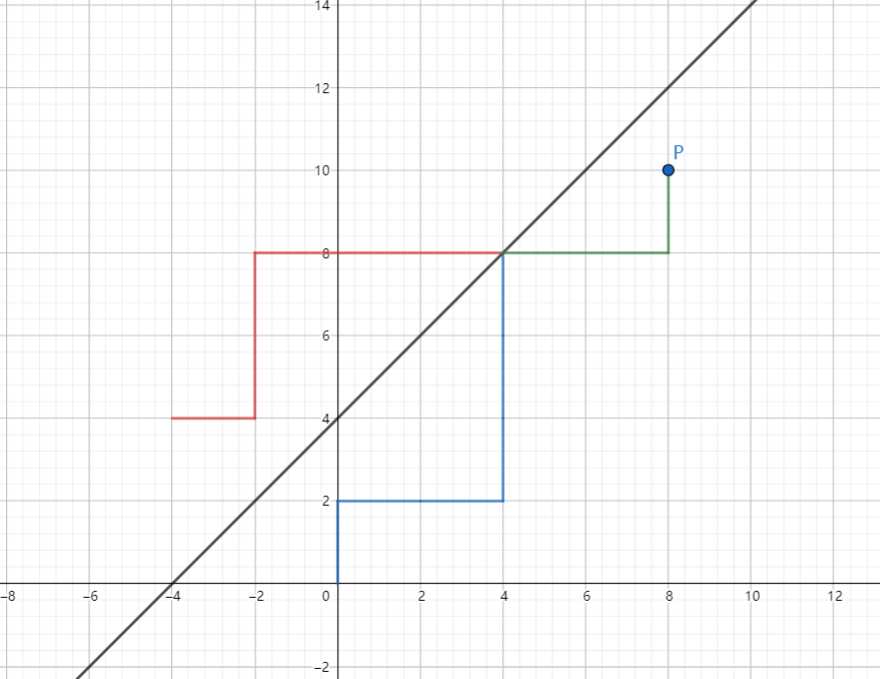
然后,这就是个十分经典的问题了:Bertrand's ballot theorem。大概可以参照下图:
先只看其中一条线的限制情况。假设 $P$ 点坐标是 $(p,q)$,那么由图中来看,在交汇点之前,红色和蓝色都是关于 $y=x+(k+1)$ 对称(因为要求可以到 $y=x+k$,那么一旦到了 $y=x+(k+1)$ 就说明穿过去了,蓝色路径不合法)从原点到 $P$ 的所有路径(包括不合法)也就是 $\binom{x+y}{y}$,不合法的路径(即红线和蓝线有交,且交完之后两线重合一直到 $P$)一共有 $\binom{x+y}{y-(k+1)}$,于是所有合法路径数就是 $\binom{x+y}{y}-\binom{x+y}{y-(k+1)}$。
那对于两条线夹着怎么办?直接上容斥!可以分别算出所有情况,减去穿过 $y=x+(k+1)$ 或 $y=x-(k+1)$ 的情况,加上穿过 $y=x+2(k+1)$ 或 $y=x-2(k+1)$ 的情况,再加......总之也就对应下面这个式子:
$$
c_k=\sum\limits_{i=L}^{R}\binom{n}{i}+2\sum\limits_{j \ge 1}(-1)^{j} \sum\limits_{i=L}^{R}\binom{n}{i-(k+1)j}
$$
其中 $L,R$ 由下列不等式算出:
$$
\left\{\begin{matrix}
x+y=n \\
y\le x+k \\
y\ge x-k
\end{matrix}\right.
$$
得到 $L=\lceil(n-k)/2\rceil,R=\lfloor(n+k)/2\rfloor$。
再回到题目中的最后要求的这个 $P\{X\le k\}$,设 $p_k$ 表示一维随机游走中满足点始终在 $[-k,k]$ 内的概率,那么就有 $p_k=\frac{c_k}{2^{n}}$,而由于两个变量相互独立,于是就有 $P\{X\le k\}=p_k^{2}$。
于是,这个题就做完啦!至于时间复杂度,首先预处理 $sc(i)=\sum_{k=0}^{i}\binom{n}{k}$,计算 $c_k$ 的复杂度是一个调和级数,于是总的时间复杂度为 $\mathcal{O}(n \log n)$。
好久没写这么长的题解了......
#include <bits/stdc++.h>
#define ll long long
#define ls id << 1
#define rs id << 1 | 1
#define mem(array, value, size, type) memset(array, value, ((size) + 5) * sizeof(type))
#define memarray(array, value) memset(array, value, sizeof(array))
#define fillarray(array, value, begin, end) fill((array) + (begin), (array) + (end) + 1, value)
#define fillvector(v, value) fill((v).begin(), (v).end(), value)
#define pb(x) push_back(x)
#define st(x) (1LL << (x))
#define pii pair<int, int>
#define mp(a, b) make_pair((a), (b))
#define Flush fflush(stdout)
#define vecfirst (*vec.begin())
#define veclast (*vec.rbegin())
#define vecall(v) (v).begin(), (v).end()
#define vecupsort(v) (sort((v).begin(), (v).end()))
#define vecdownsort(v, type) (sort(vecall(v), greater<type>()))
#define veccmpsort(v, cmp) (sort(vecall(v), cmp))
using namespace std;
const int N = 1000050;
const int inf = 0x3f3f3f3f;
const ll llinf = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
int MOD = 1e9 + 7;
const double PI = acos(-1.0);
clock_t TIME__START, TIME__END;
void program_end()
{
#ifdef ONLINE
printf("\n\nTime used: %.6lf(s)\n", ((double)TIME__END - TIME__START) / 1000);
system("pause");
#endif
}
ll ksm(ll a, ll b, int mod2=MOD)
{
ll ret = 1;
while (b)
{
if (b & 1)
ret = ret * a % mod2;
a = a * a % mod2;
b >>= 1;
}
return ret;
}
int n;
int fac[N],invfac[N],sumC[N];
int C(int n,int m){return n<m?0:1ll*fac[n]*invfac[n-m]%MOD*invfac[m]%MOD;}
int ans;
void init()
{
fac[0]=1;for(int i=1;i<=n;++i)fac[i]=1ll*fac[i-1]*i%MOD;
invfac[n]=ksm(fac[n],MOD-2);for(int i=n-1;i>=1;--i)invfac[i]=1ll*invfac[i+1]*(i+1)%MOD;int inv2=(MOD+1)/2;
sumC[0]=C(n,0);for(int i=1;i<=n;++i)sumC[i]=(1ll*sumC[i-1]+C(n,i))%MOD;
ans=n;invfac[0]=1;
}
int add(int a, int b, int p = MOD) { return (a += b) >= p ? a -= p : a; }
int sub(int a, int b, int p = MOD) { return (a -= b) < 0 ? a += p : a; }
int mul(ll a, ll b, int p = MOD) { return add(a * b % p, p); }
int calck(int k)
{
int L=(n-k+1)/2,R=(n+k)/2;
int ret=sub(sumC[R],sumC[L-1]);
int res=0;
for(int j=1;(k+1)*j<=R;++j)
{
if(j&1)res=sub(res,sub(sumC[R-(k+1)*j],L-1-(k+1)*j<0?0:sumC[L-1-(k+1)*j]));
else res=add(res,sub(sumC[R-(k+1)*j],L-1-(k+1)*j<0?0:sumC[L-1-(k+1)*j]));
}
res=mul(res,2);
ret=add(ret,res);
return ret;
}
inline void solve()
{
scanf("%d%d",&n,&MOD);
init();int res=0;int mu=ksm(ksm(2,2*n),MOD-2);
for(int k=1;k<n;++k)
{
int ck=calck(k);
ck = mul(ck,ck);
ck=mul(ck,mu);
res=add(res,ck);
}
cout<<sub(ans,res)<<'\n';
}
int main()
{
TIME__START = clock();
int Test = 1;
scanf("%d", &Test);
while (Test--)
{
solve();
// if (Test)
// putchar('\n');
}
TIME__END = clock();
program_end();
return 0;
}






Comments NOTHING