Kruskal重构树学习笔记

发布于 2021-01-04  11 次阅读

这个东西可以用来搞一搞图的连通性啊，在最小 / 最大生成树上维护一些东西的时候可以用到。

构造方法：进行 kruskal 的过程中，对于可以合并的一条边的两个节点所在的集合的根节点，新开一个节点（表示这条边），然后这个节点就作为这俩根节点的父亲节点，这样形成的一棵树就是 kruskal 重构树。其中这条边的边权化为这个新节点的点权。

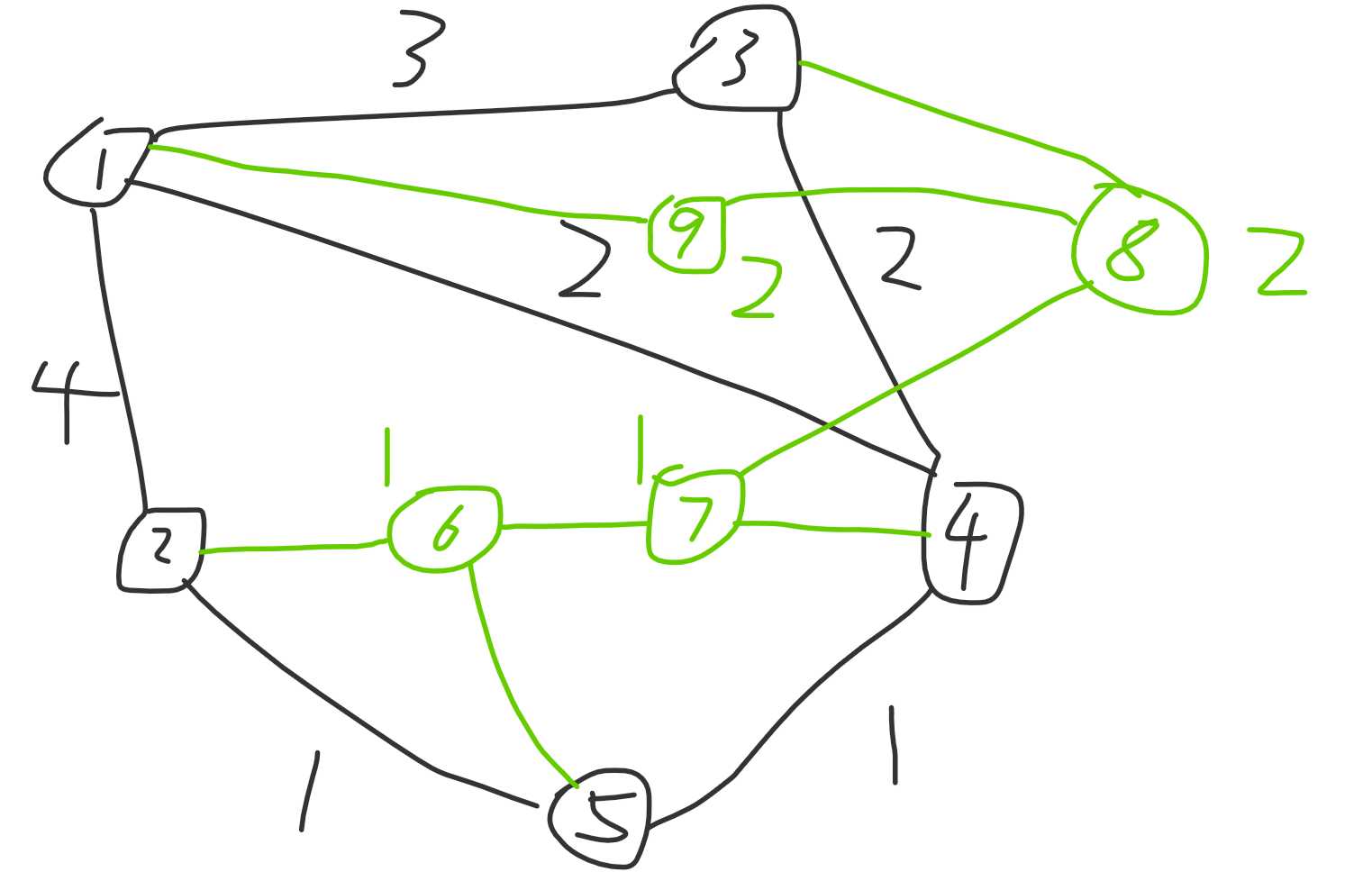
说起来有点抽象，不如来直接看图：

（画得很丑见谅......）

按照 kruskal 算法的流程，每条边按照权值排序之后依次把两个点尝试合并到一个集合内，如果本来就在一个集合就不合并。

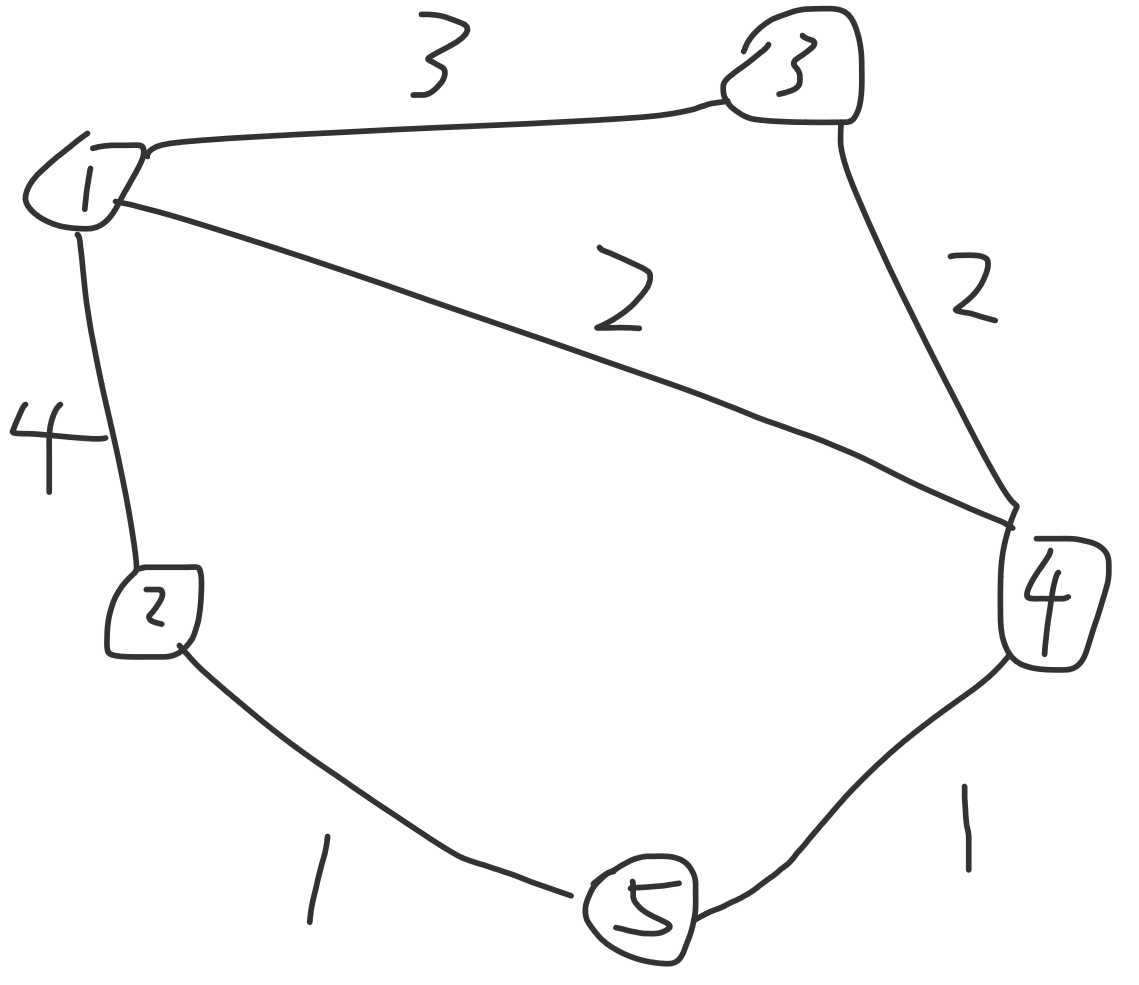
第一次合并之后结果如图：

绿色的那个点就是新建的点，点权就是 <2,5> 这条边的边权。

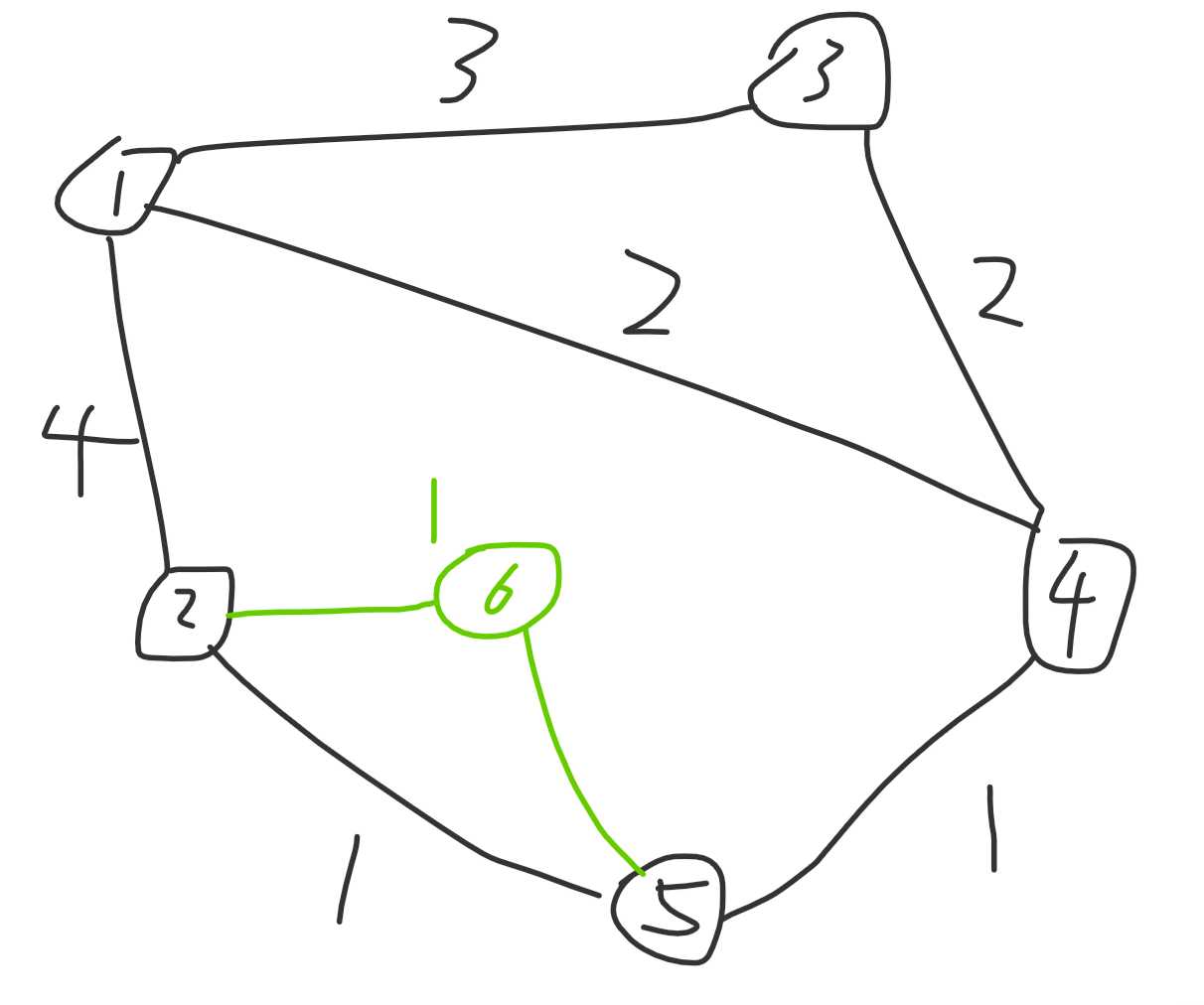
第二次合并之后如图：

第二次找到的边是 <4,5> 这条，然后 5 被合并过，其对应的根节点为 6，这个时候就需要把 6 和 4 合并，并把新节点 7 作为 4 和 6 的父亲，点权就是 <4,5> 的边权。

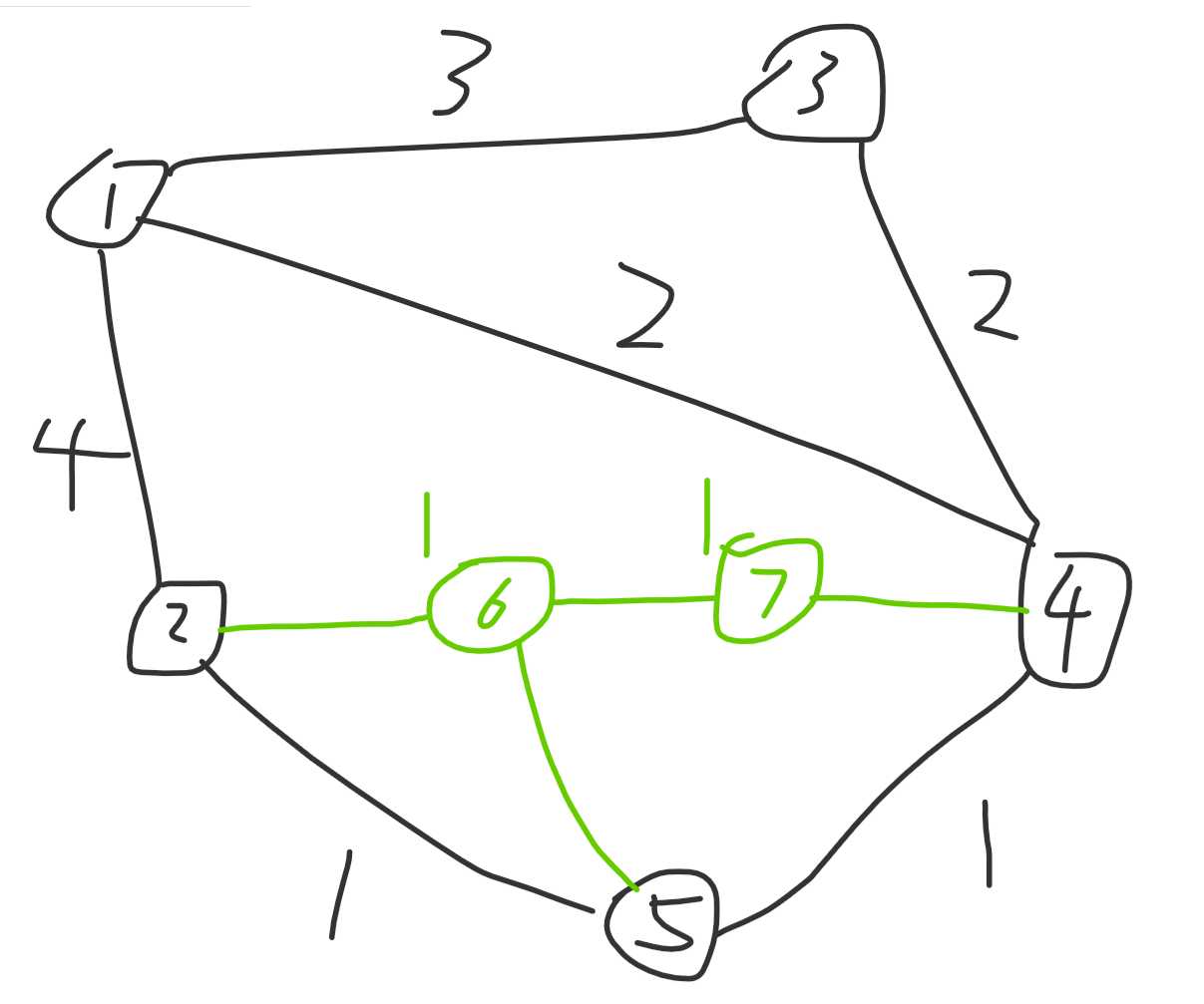
之后的合并就依此类推，第三次合并之后如图：

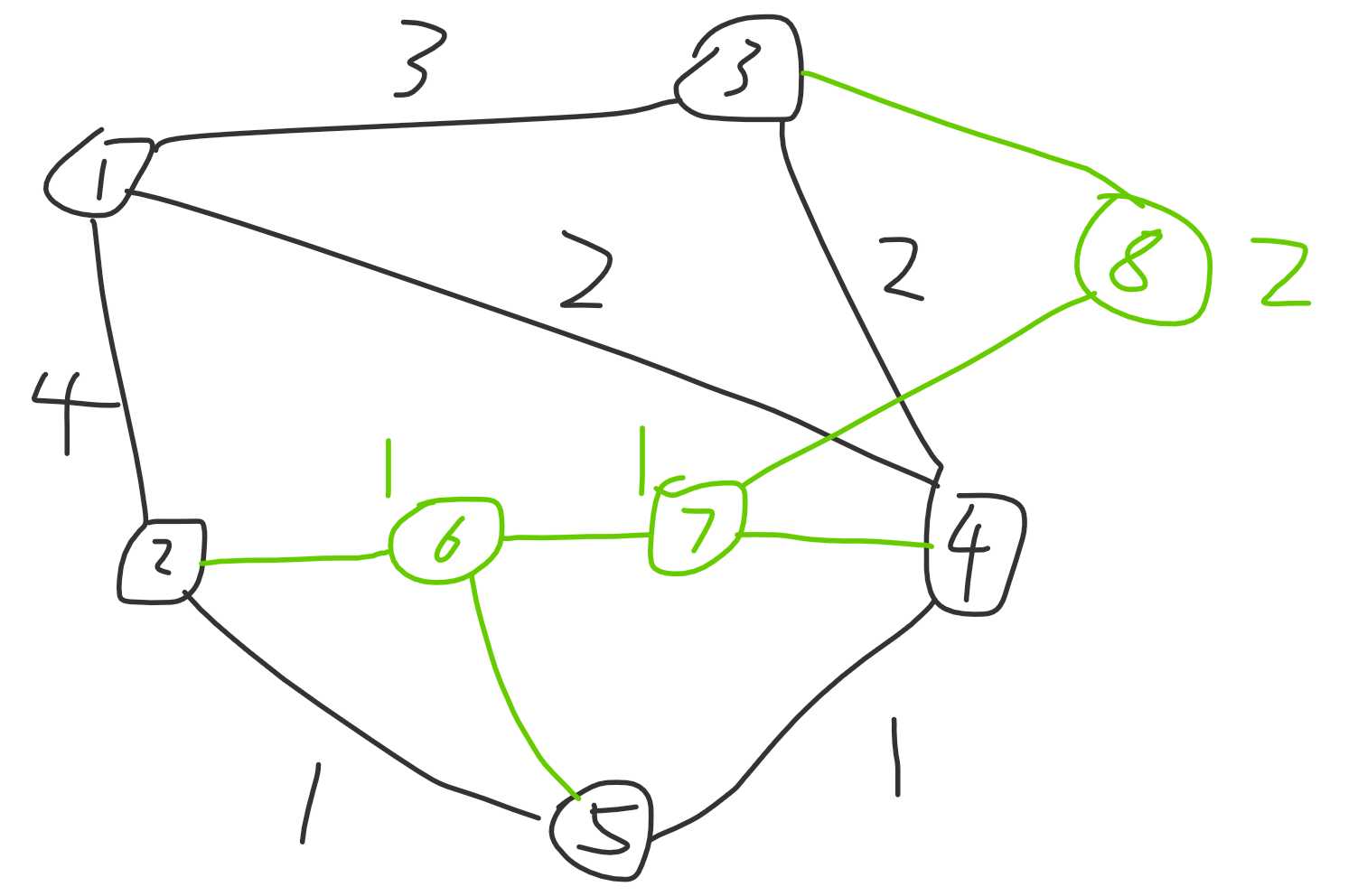
第四次合并之后如图：

这个时候，所有的点都被合并上了，至此，重构树就构造好了。

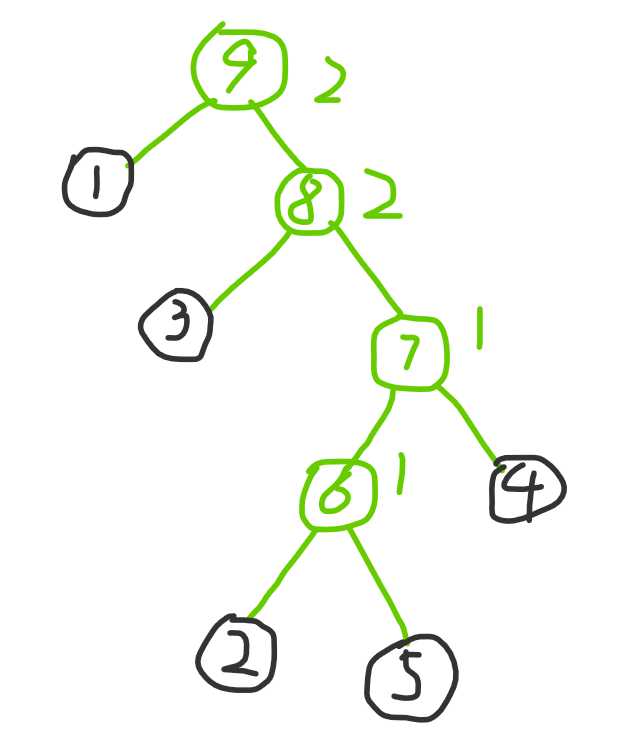
当然直接看这个图还是挺难看的......把重构树单独提取出来看看？

这个图就极其直观了：

  1. 显然是二叉树，满足大根堆的性质（即父亲的点权大于等于左右儿子的权值）；
  2. 原图的节点都是叶子节点；
  3. 两个叶子的 LCA 的权值就是：从 u 点走到 v 点的所有路径中，经过的最大边权最小是多少。

然后就可以对这棵树进行各种维护了......比如跑个 dfs 序然后上线段树啊，比如树上倍个增啊什么的。

而且，这个东西可以一定程度上维护图的连通性（当然，没有 LCT 那么强大）。

来看些例题吧

NOI2018 D1T1 归程

也算是很经典的一个题了吧~

首先可以 dijkstra 求出每个点到 1 的最短路，之后按照海拔从大到小对边排序，建出 kruskal 重构树，不难发现对于低于特定的海拔，一个点能够到达的点集在重构树上他们都在同一棵子树内。所以就可以用线段树维护 dfs 序，然后每次询问需要找到 v 这个叶子上对应的海拔恰好大于 p 的最近的祖先，这个直接倍增往上跳就可以了。线段树维护的就是最短路 dis 的最小值。

这个题就很愉快地做完了~时间复杂度为 $\mathcal{O}(T(n\log n+Q\log n))$

#include <bits/stdc++.h>
#define ll long long
#define ls id << 1
#define rs id << 1 | 1
#define mem(array, value, size, type) memset(array, value, ((size) + 5) * sizeof(type))
#define memarray(array, value) memset(array, value, sizeof(array))
#define fillarray(array, value, begin, end) fill((array) + (begin), (array) + (end) + 1, value)
#define fillvector(v, value) fill((v).begin(), (v).end(), value)
#define pb(x) push_back(x)
#define st(x) (1LL << (x))
#define pii pair<int, int>
#define mp(a, b) make_pair((a), (b))
#define Flush fflush(stdout)
#define vecfirst (*vec.begin())
#define veclast (*vec.rbegin())
#define vecall(v) (v).begin(), (v).end()
#define vecupsort(v) (sort((v).begin(), (v).end()))
#define vecdownsort(v, type) (sort(vecall(v), greater<type>()))
#define veccmpsort(v, cmp) (sort(vecall(v), cmp))
using namespace std;
const int N = 500050;
const int inf = 0x3f3f3f3f;
const ll llinf = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
clock_t TIME__START, TIME__END;
void program_end()
{
#ifdef VINGYING
    printf("\n\nTime used:
    system("pause");
#endif
}
int n, m, f[N], in[N], out[N], tim, dep[N];
ll p[N][20], a[N], father[N][20];
int Find(int x) { return x == f[x] ? x : f[x] = Find(f[x]); }
vector<int> e2[N];
bool Union(int x, int y, ll height)
{
    int fx = Find(x), fy = Find(y);
    if (fx != fy)
    {
        n++;
        f[n] = n, f[fx] = n, f[fy] = n;
        e2[n].push_back(fy);
        e2[n].push_back(fx);
        a[n] = height;
        return true;
    }
    return false;
}
void dfs(int u, int fa)
{
    in[u] = ++tim;
    dep[u] = dep[fa] + 1;
    father[u][0] = fa;
    p[u][0] = a[fa];
    for (int i = 1; i < 20; ++i)
    {
        p[u][i] = p[father[u][i - 1]][i - 1];
        father[u][i] = father[father[u][i - 1]][i - 1];
    }
    for (auto v : e2[u])
    {
        if (v == fa)
            continue;
        dfs(v, u);
    }
    out[u] = tim;
}
int jump(int u, ll height)
{
    for (int i = 19; i >= 0; --i)
    {
        if (dep[u] - st(i) > 0 && p[u][i] > height)
            u = father[u][i];
    }
    return u;
}
struct edge
{
    int u, v;
    ll length, height;
} e[N];
bool cmpedge(const edge &x, const edge &y) { return x.height > y.height; }
vector<edge> g[N];
ll dis[N];
bool vis[N];
struct node
{
    int u;
    ll length;
    bool operator<(const node &x) const
    {
        return length > x.length;
    }
};
void dijkstra()
{
    priority_queue<node> pq;
    mem(dis, inf, n, ll);
    mem(vis, 0, n, bool);
    dis[1] = 0;
    pq.push((node){1, 0});
    while (!pq.empty())
    {
        node u = pq.top();
        pq.pop();
        if (vis[u.u])
            continue;
        vis[u.u] = 1;
        for (auto v : g[u.u])
        {
            if (dis[v.v] > dis[u.u] + v.length)
            {
                dis[v.v] = dis[u.u] + v.length;
                pq.push((node){v.v, dis[v.v]});
            }
        }
    }
}
struct segtree
{
    int l, r;
    ll mn;
} t[N << 2];
inline void pushup(int id) { t[id].mn = min(t[ls].mn, t[rs].mn); }
void build(int l, int r, int id)
{
    t[id].l = l, t[id].r = r, t[id].mn = llinf;
    if (l == r)
        return;
    int mid = (l + r) >> 1;
    build(l, mid, ls);
    build(mid + 1, r, rs);
}
void change(int pos, ll val, int id)
{
    int l = t[id].l, r = t[id].r;
    if (l == r)
    {
        t[id].mn = val;
        return;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid)
        change(pos, val, ls);
    else
        change(pos, val, rs);
    pushup(id);
}
ll query(int L, int R, int id)
{
    int l = t[id].l, r = t[id].r;
    if (L <= l && R >= r)
        return t[id].mn;
    int mid = (l + r) >> 1;
    if (R <= mid)
        return query(L, R, ls);
    else if (L > mid)
        return query(L, R, rs);
    else
        return min(query(L, mid, ls), query(mid + 1, R, rs));
}

void data_clear()
{
    memarray(a, inf);
    for (int i = 0; i <= n; ++i)
        e2[i].clear(), g[i].clear();
    tim = 0;
}

inline void solve()
{
    scanf(
    int nn = n;
    for (int i = 1; i <= m; ++i)
    {
        int u, v, l, a;
        scanf(
        e[i].height = a, e[i].length = l, e[i].u = u, e[i].v = v;
        g[u].push_back((edge){u, v, l, a});
        g[v].push_back((edge){v, u, l, a});
    }
    dijkstra();
    sort(e + 1, e + m + 1, cmpedge);
    for (int i = 1; i <= n; ++i)
        f[i] = i;
    int tot = 0;
    for (int i = 1; i <= m; ++i)
    {
        int x = e[i].u, y = e[i].v, h = e[i].height;
        tot += Union(x, y, h);
        if (tot == nn - 1)
            break;
    }
    for (int i = 1; i <= n; ++i)
        if (Find(i) == i)
            dfs(i, 0);
    build(1, tim, 1);
    for (int i = 1; i <= nn; ++i)
        change(in[i], dis[i], 1);
    int Q, K, S;
    ll lastans = 0;
    scanf(
    while (Q--)
    {
        int v, p;
        scanf(
        v = (v + K * lastans - 1)
        int u = jump(v, p);
        ll ans = query(in[u], out[u], 1);
        lastans = ans;
        printf(
    }
    data_clear();
}

int main()
{
    // freopen("return.in", "r", stdin);
    // freopen("return.out", "w", stdout);
    TIME__START = clock();
    int Test = 1;
    scanf(
    while (Test--)
    {
        solve();
        // if (Test)
        //     putchar('\n');
    }
    TIME__END = clock();
    program_end();
    return 0;
}

Codeforces 1416D - Graph and Queries

这个题需要搞搞连通性......

如果把两个连通分量的重构树连起来的话，不难发现连通分量各自内部的 dfs 序是不会变的，那么这个题就可以把所有操作都倒过来，删边变成加边。

先求出所有操作弄完之后的每个连通分量的 kruskal 重构树，之后倒过来每次加边就还是按照重构树那样来构造，只不过这样可以保证 dfs 序不会乱。

倒过来加边处理完之后，可能最后还是有多个连通分量，每个连通分量求一次 dfs 序即可。所有的 dfs 序放在线段树上一起维护即可。

然后对于操作 1 倒过来的话，可以看成每次操作都是去查询这个连通分量的并查集的根节点，那就直接把查询的这个点变成当前集合的根节点即可。这样后续加边的时候这个点会转移到这个连通分量的子树的根上，方便后面的操作正序过来的询问。

总之，在构建 kruskal 重构树的时候，顺序是很重要的！一定要理清楚每一步的意义！

#include <bits/stdc++.h>
#define ll long long
#define ls id << 1
#define rs id << 1 | 1
#define mem(array, value, size, type) memset(array, value, ((size) + 5) * sizeof(type))
#define memarray(array, value) memset(array, value, sizeof(array))
#define fillarray(array, value, begin, end) fill((array) + (begin), (array) + (end) + 1, value)
#define fillvector(v, value) fill((v).begin(), (v).end(), value)
#define pb(x) push_back(x)
#define st(x) (1LL << (x))
#define pii pair<int, int>
#define mp(a, b) make_pair((a), (b))
#define Flush fflush(stdout)
#define vecfirst (*vec.begin())
#define veclast (*vec.rbegin())
#define vecall(v) (v).begin(), (v).end()
#define vecupsort(v) (sort((v).begin(), (v).end()))
#define vecdownsort(v, type) (sort(vecall(v), greater<type>()))
#define veccmpsort(v, cmp) (sort(vecall(v), cmp))
using namespace std;
const int N = 1000050;
const int inf = 0x3f3f3f3f;
const ll llinf = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
clock_t TIME__START, TIME__END;
void program_end()
{
#ifdef ONLINE
    printf("\n\nTime used:
    system("pause");
#endif
}
int n, m, Q, p[N], f[N], in[N], out[N], tim, del[N];
vector<int> g[N];
int Find(int x) { return x == f[x] ? x : f[x] = Find(f[x]); }
void Union(int x, int y)
{
    int fx = Find(x), fy = Find(y);
    if (fx != fy)
    {
        ++n;
        f[n] = n, f[fx] = n, f[fy] = n;
        g[n].push_back(fx), g[n].push_back(fy);
    }
}
void dfs_tim(int u, int fa)
{
    in[u] = ++tim;
    for (auto v : g[u])
    {
        if (v != fa)
            dfs_tim(v, u);
    }
    out[u] = tim;
}
struct querys
{
    int type;
    int val;
} q[N];
struct edges
{
    int u, v;
} e[N];
struct segtree
{
    int l, r;
    pii mx;
} t[N << 2];
inline void pushup(int id) { t[id].mx = max(t[ls].mx, t[rs].mx); }
void build(int l, int r, int id)
{
    t[id].l = l, t[id].r = r;
    if (l == r)
        return;
    int mid = (l + r) >> 1;
    build(l, mid, ls);
    build(mid + 1, r, rs);
}
void change(int pos, pii val, int id)
{
    int l = t[id].l, r = t[id].r;
    if (l == r)
    {
        t[id].mx = val;
        return;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid)
        change(pos, val, ls);
    else
        change(pos, val, rs);
    pushup(id);
}
pii query(int L, int R, int id)
{
    int l = t[id].l, r = t[id].r;
    if (L <= l && R >= r)
        return t[id].mx;
    int mid = (l + r) >> 1;
    if (R <= mid)
        return query(L, R, ls);
    else if (L > mid)
        return query(L, R, rs);
    else
        return max(query(L, mid, ls), query(mid + 1, R, rs));
}

inline void solve()
{
    scanf(
    int nn = n;
    for (int i = 1; i <= n; ++i)
        scanf(
    for (int i = 1; i <= m; ++i)
    {
        int x, y;
        scanf(
        e[i] = (edges){x, y};
    }
    for (int i = 1; i <= Q; ++i)
    {
        scanf(
        if (q[i].type == 2)
            del[q[i].val] = 1;
    }
    for (int i = 1; i <= m; ++i)
        if (del[i] == 0)
            Union(e[i].u, e[i].v);
    for (int i = Q; i; --i)
    {
        if (q[i].type == 2)
            Union(e[q[i].val].u, e[q[i].val].v);
        else
            q[i].val = Find(q[i].val);
    }
    for (int i = 1; i <= n; ++i)
        if (Find(i) == i)
            dfs_tim(i, 0);
    build(1, tim, 1);
    for (int i = 1; i <= nn; ++i)
        change(in[i], mp(p[i], i), 1);
    for (int i = 1; i <= Q; ++i)
    {
        if (q[i].type == 1)
        {
            int u = q[i].val;
            pii ans = query(in[u], out[u], 1);
            printf(
            int node = ans.second;
            if (in[node])
                change(in[node], mp(0, 0), 1);
        }
    }
}

int main()
{
    TIME__START = clock();
    int Test = 1;
    // scanf(
    while (Test--)
    {
        solve();
        // if (Test)
        //     putchar('\n');
    }
    TIME__END = clock();
    program_end();
    return 0;
}

总而言之，kruskal 重构树可以处理最小 / 最大生成树的一些问题，可以套 dfs 序、线段树什么的来维护一些东西，将边权转为点权来实现，较为方便。

并且一定要注意顺序！