2019-2020 ICPC, NERC, Southern and Volga Russian Regional Contest 题解

## A - [Berstagram](https://codeforces.com/contest/1250/problem/A)
### 题目大意
现在有一个序列 $1,2,...,n-1,n$，有 $m$ 次操作，每次可以把其中一个数往前挪一位（如果这个数在第一位就不动）。问每个数可能在这个序列的最左边和最右边分别是多少？
$1 \leq n \leq 10^5,1 \leq m \leq 4 \times 10^5$
### 思路简述
直接根据题意模拟就行了......
[Code by HeRaNO](https://github.com/HeRaNO/OI-ICPC-Codes/blob/master/Codeforces/1250A.cpp)
## B - [The Feast and the Bus](https://codeforces.com/contest/1250/problem/B)
### 题目大意
现在有 $n$ 个人属于不同的 $k$ 个小组。现在你只有一辆车，但你可以选择在这车上安装 $s$ 个位置。现在要把这 $n$ 个人都运走，出发一次需要的花费为 $s$，并且一个小组内的人不能被分开来运。问如何选择 $s$，使得总花费最少？输出总花费。
$1 \leq n \leq 5\times 10^5,1 \leq k \leq 8000$
### 思路简述
显然，这个题不能二分这个 $s$，因为设运的次数为 $t$，那么总花费就是 $s\times t$，而 $t$ 与 $s$ 有关，所以不具有二分性。
这个题可以考虑贪心：将每一组的人数从大到小排序后，实际上我们只需要从头和尾开始往中间逼近，设 $c_i$ 表示第 $i$ 组的人数，那么我们就需要找最大的 $c_i+c_j$，这就是我们需要找的 $s$。之后仍然是双指针那样，从头和尾开始，根据这个 $s$ 来更新答案就行。
[Code by Vingying](https://github.com/HeRaNO/OI-ICPC-Codes/blob/master/Codeforces/1250B.cpp)
## C - [Trip to Saint Petersburg](https://codeforces.com/contest/1250/problem/C)
### 题目大意
一个人想去圣彼得堡旅游，他从第 $L$ 天去并在第 $R$ 天回来，每一天花费 $k$ 块钱。现在他要在圣彼得堡兼职赚钱，现在一共有 $n$ 份兼职，第 $i$ 份兼职从第 $l_i$ 天开始，第 $r_i$ 天结束，并且获得 $p_i$ 块钱。他可以一次性做很多份兼职，但每一份兼职必须从头做到尾，否则不能得钱。问：他该如何选择 $L,R$，使得自己能够赚钱，并且赚得最多？盈利为 $0$ 或者亏损输出 $-1$。
$1 \leq n \leq 2\times 10^5,1 \leq k,p_i \leq 10^{12}, 1 \leq l_i \leq r_i \leq 2\times 10^5$
### 思路简述
这个题还要输出方案......
首先不难发现，我们要找的 $L,R$ 一定是某一份工作的 $l_i$ 和某一份工作的 $r_i$ 。我们可以将每一份工作按照 $l_i$ 排序，将每一份工作看做一条线段，这样实际上就是左端点枚举，动态删除线段，查询最大和的经典问题了。这一部分可以用前缀和+线段树区间加以及区间最大来实现。然后这个题还要输出方案，所以线段树里面存一个pair，表示最大和以及对应的右端点就行。
[Code by Vingying](https://github.com/HeRaNO/OI-ICPC-Codes/blob/master/Codeforces/1250C.cpp)
## D - [Conference Problem](https://codeforces.com/contest/1250/problem/D)
一道神仙dp好像......还没看题
## E - [The Coronation](https://codeforces.com/contest/1250/problem/E)
~~（这题真是苦了xydg了）~~
### 题目大意
有 $n$ 个人，第 $i$ 个人佩戴着第 $i$ 个宝石项链，每一个宝石项链都由 $m$ 个宝石组成。宝石一共有两种，”0“表示第一种，”1“表示另外一种。如果 $i$ 和 $j$ 佩戴的宝石项链相同位置上宝石种类相同数小于 $k$，那么这两个人就会发生冲突。现在你可以让一些人反着戴宝石项链，例如00101110反着戴为01110100。问是否可以让所有人互相都不起冲突？如果不可以，输出 $-1$；如果可以，则输出最少需要反戴的人数以及一个方案。
$2 \leq n \leq 50,1 \leq k \leq m \leq 50$
### 思路简述
我们来看第 $i$ 个人和第 $j$ 个人的情况：
1. 两个人无论是否反不反戴，都不会起冲突；
2. 两个人无论是否反不反戴，都会起冲突。这种情况便是无解，直接输出$-1$即可；
3. 两个人都不反戴会起冲突，其中一个人反戴不会起冲突。
对于每一个项链，都有两种状态：反戴与不反戴，设不反戴的状态为 $i$，反戴的状态为 $i'$，那么我们可以讨论每一种情况：
1. $i$ 和 $j$ 是不冲突的，$i'$ 和 $j'$ 也是不冲突的；
2. 输出$-1$；
3. $i$ 和 $j'$ 是不冲突的，$i'$ 和 $j$ 是冲突的。
这其实和2-SAT有些像，我们可以按照2-SAT的构图方式去建图，然后每一个连通块里面统计一个答案即可。
~~だが断る！~~
使用 2-SAT 去处理这个问题的话有一个缺点，就是 2-SAT 并不是直接得出代价最小的方案。所以我们可以寻求一个相似的替代方案。
实际上根据上面的分析，直接搞二分图，对每个连通块分别处理，dfs染色即可。
在染色完成之后，对于每个联通块统计一下两种染色方案哪一种的代价更小，然后选取更小的方案即可。由于联通块之间的选择互相之间不影响，所以可证这是最优的。
[Code by ZXyang](https://github.com/HeRaNO/OI-ICPC-Codes/blob/master/Codeforces/1250E.cpp)
## F - [Data Center](https://codeforces.com/contest/1250/problem/F)
这题就十足的签到题了（
[Code by Vingying](https://github.com/HeRaNO/OI-ICPC-Codes/blob/master/Codeforces/1250F.cpp)
## G - [Discarding Game](https://codeforces.com/contest/1250/problem/G)
### 题目大意
你和电脑做游戏。游戏一共有 $n$ 轮，第 $i$ 轮你会得到 $a_i$ 分，电脑会得到 $b_i$ 分。当有一方的分数大于等于 $k$ 时这一方输掉（你和电脑可能同时输掉）。现在你有一种操作，每次操作可以让双方减去目前双方较小的分数。问你是否能赢？不能输出$-1$，能的话输出最小需要的操作次数，并且输出一个方案。
$1\leq n \leq 2\times 10^5,2 \leq a_i,b_i < k \leq 10^9$
### 思路简述
假设现在游戏进行到了第 $i$ 轮，那么我在第 $i$ 轮进行一次操作，在第 $i+1$ 轮进行一次操作，等价于在第 $i+1$ 轮进行一次操作（当然，第 $i$ 轮时你输了除外）。于是我们可以用单调队列，或者尺取法来进行一次 $O(n)$ 的dp，设 $dp[i]$ 表示前 $i$ 轮所需要的最小操作次数，那么转移就是 $dp[i]=dp[j]+1$。
dp之后就是更新答案。 更新答案的过程也和上述dp过程异曲同工，然后这题要输出方案，dp的时候记录一下dp的前驱就行。
[Code by Vingying](https://github.com/HeRaNO/OI-ICPC-Codes/blob/master/Codeforces/1250G.cpp)
## H - [Happy Birthday](https://codeforces.com/contest/1250/problem/H)
### 题目大意
给你 $c_0$ 个 $0$，$c_1$ 个 $1$，......，$c_9$ 个 $9$，你所不能组出的最小的不含前导0的正整数是什么？
$0 \leq c_i \leq 10^5$
### 思路简述
一个简单的分类讨论。
我们只需要找出第一个出现次数 $cnt$ 最小的那个数，之后输出 $cnt+1$ 次该数就行。当然这是不考虑有 $0$ 的情况。有 $0$ 的话就看 $0$ 的出现次数 $cnt_0$ 与 $cnt$ 的大小，如果 $cnt_0+1<cnt$ 那么就输出这个数后补上 $cnt_0+1$ 个 $0$ 就行。
[Code by Vingying](https://github.com/HeRaNO/OI-ICPC-Codes/blob/master/Codeforces/1250H.cpp)
## I - [Show Must Go On](https://codeforces.com/contest/1250/problem/I)
好像也是一个神仙dp......还没看
## J - [The Parade](https://codeforces.com/contest/1250/problem/J)
### 题目大意
所有的士兵身高种数为 $n$，身高为 $i$ 的士兵有 $c_i$ 个。现在要将这些士兵排成 $k$ 排，每一排的士兵两两身高差的绝对值不能超过 $1$。现问最多可以排多少士兵？
$1 \leq n \leq 30000,1 \leq k,c_i \leq 10^{12}$
### 思路简述
显然答案是有二分性的，我们可以二分每一排有多少个士兵，然后check就行。
怎么check呢？我们不可能一排一排地放，而是从身高小的往大的排，这样可以保证是最优的排法。于是就只需要看这个身高的可以排多少排，然后依次这么处理过去即可。
[Code by Vingying](https://github.com/HeRaNO/OI-ICPC-Codes/blob/master/Codeforces/1250J.cpp)
## K - [Projectors](https://codeforces.com/contest/1250/problem/K)
貌似是一道神仙网络流......还没看（
## L - [Divide The Students](https://codeforces.com/contest/1250/problem/L)
### 题目大意
一共有 $a$ 个学生用汇编，$b$ 个学生用 Basic，$c$ 个学生用 C++，要把他们分成三组，求在所有分组方案中人数最多的组的最少人数。
$1 \leq a,b,c \leq 1000$
### 思路简述
枚举答案，现在要把会 Basic 的学生分到 $a$ 和 $c$ 里，先判断 $a$ 和 $c$ 是不是要进到 $b$ 里面，然后进多少。
[Code by ZXyang](https://github.com/HeRaNO/OI-ICPC-Codes/blob/master/Codeforces/1250L.cpp)
## M - [SmartGarden](https://codeforces.com/contest/1250/problem/M)
### 题目大意
有这么一块 $n\times n$ 的农田（图为 $n=5$ 的情况）
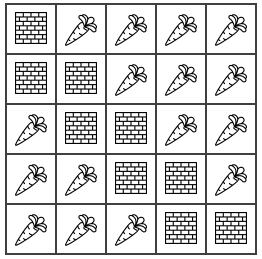
主对角线以及下面那条对角线全是石块，现在你可以做最多 $50$ 次操作，每次操作可以选取一些行和列，之后在这些行和列的交叉点给农作物浇水。注意不可以选取交叉点有石块的行和列。输出一种让所有农作物都至少被浇过一次水的方案。
$1 \leq n \leq 5000$
### 思路简述
这题好神奇啊......智慧的构造。
这里翻译一下 zscoder 的题解（
For each bit $i$, let L = set of indices $x$ with bit $i=0$, R = set of indices $y$ with bit $i=1$ and $y+1$ also has bit $i=1$.
Similarly, for each bit $i$, let L = set of indices $x$ with bit $i=1$, R = set of indices $y$ with bit $i=1$ and $y+1$ also has bit $i=0$.
Now, we used 26 sets.
Observe that only pairs $(x,y)$, with $y = 01111...1$ (the string of 1s is nonempty) and $x = 1$ such that there is at least one bit 1 in the suffix, are uncovered.
Thus, it is sufficient to make $12$ more queries that cover all $y$ of the form $0111...1$ for a fixed 1-suffix length and then put all $x$ that can be matched on the left hand side.
In total, my solution uses $38$ queries.
对于每一位 $i$，让 $L$ 为所有第 $i$ 位为 $0$ 的 $x$ 坐标的集合，让 $R$ 为所有第 $i$ 位为 $1$ 并且 $y+1$ 的第 $i$ 位也为 $1$ 的 $y$ 坐标的集合；
相似地，让 $L$ 为所有第 $i$ 位为 $1$ 的 $x$ 坐标的集合，让 $R$ 为所有第 $i$ 位为 $0$ 并且 $y+1$ 的第 $i$ 位也为 $0$ 的 $y$ 坐标的集合。
现在，我们有 $26$ 个集合了。
注意到只有形如 $(x,y)$ 的点对，其中 $y=0111...1$（“1”串非空）并且 $x=1$ ，这样至少有一个“1”在后缀没有被覆盖。
因此，可以构造 $12$ 次操作覆盖所有对于一个固定“1”串长度，形如 $0111...1$ 的 $y$，之后构造所有满足条件的 $x$。
总计，操作数为 $38$ 次。
~~渣翻见谅~~
## N - [Wires](https://codeforces.com/contest/1250/problem/N)
### 题目大意
给定由 $n$ 个点组成的若干个无向边构成的连通块，希望修改最少的边使得所有的**边**是互达的（即边连通），并输出一个方案。
$1\leq n \leq 10^5$
### 思路简述
可以发现连通图要么带环，要么是一棵树。也不难发现，最少修改次数就是初始连通块数量-1.
如果一个连通块里面有度数为 $1$ 的点，就直接将与它相连的边修改就行。
而如果没有的话，就说明这个连通块肯定带环，直接改一条环边就行。
~~然而这题真的不好写~~
[ZXyang](https://acm.uestc.edu.cn/user/ZXyaang/ ): 一开始想的是暴力模拟找叶结点和环，但是这个样子写起来会非常非常麻烦。于是在wa了两发之后，我突发奇想换了一种写法，就变成代码里面既可以找叶结点又可以找环的神奇dfs了。
即：直接dfs随便走，直到走到了一个结点没有任何未访问过的节点相连接，那么这个点要不是叶节点，要不然就是在环上的节点。
[Code by ZXyang](https://github.com/HeRaNO/OI-ICPC-Codes/blob/master/Codeforces/1250N.cpp)
## 总结
~~奇怪的知识增加了！~~